Understanding how to calculate loan interest is critical for borrowers to make sound financial decisions. Whether you’re taking out a mortgage, personal loan, or auto loan, understanding the interest calculation process allows you to analyze the total cost of borrowing and plan your repayment strategy successfully.
This article provides a thorough overview of how to figure out the interest on a loan, encompassing various loan kinds, formulae, real-world examples, and helpful advice.
Interest on a loan is calculated based on the principal, interest rate, and time period.
What Is the Interest on a Loan?
The extra cost or fee lenders impose for borrowing money is called interest on a loan. It is the fee for the right to use another person’s money. Interest is often added to the entire payback amount and is calculated as a percentage of the loan principal. There are several official loan interest calculators available on the internet which can help you calculate the interest.
Understanding Loan Basics
Types of loans
Fixed-Rate Loans: With fixed-rate loans, your monthly payments remain the same because the interest rate is constant during the loan. Since the interest rate doesn’t change the state of the market, these loans offer stability and certainty.
Variable-Rate Loans: Loans with variable rates, commonly called adjustable-rate loans, have an interest rate subject to fluctuation. Usually, an index, such as the prime rate or the London Interbank Offered Rate (LIBOR), links the interest rate. This loan is subject to interest rate adjustments, which can alter monthly payments.
Loan Terms and Conditions
- Principal Amount: The initial amount borrowed from the lender is the principal amount. It serves as the foundation for figuring out interests.
- Interest Rate: The percentage added to the principal to calculate the interest payable is the interest rate. An annual percentage rate (APR) is typically used to express it.
- Loan Term: The agreed-upon time frame for loan repayment is the loan term. The amount of monthly payments and the total amount of interest paid are impacted.
- Repayment Schedule: The repayment plan specifies the amount and frequency of payments that must be made throughout the loan period. Depending on the sort of loan, it can be different, with monthly, bimonthly, or quarterly payments possible.
Simple Interest Calculation
Formula for Simple Interest
Simple Interest (SI) = (Principal × Interest Rate × Time) / 100
Step-by-Step Calculation Process
- Identify the principal amount, interest rate, and period for calculating interest.
- Convert the interest rate into a decimal form (divide by 100).
- Multiply the principal amount by the interest rate and the period.
- Divide the result by 100 to obtain the simple interest.
Example #1: Calculating Simple Interest on a Fixed-Rate Loan
Let’s consider a scenario where you borrow $10,000 at an interest rate of 5% for 2 years.
Step 1: Principal = $10,000
Step 2: Interest Rate = 5% = 0.05 (decimal form)
Step 3: Time = 2 years
Simple Interest (SI) = (10,000 × 0.05 × 2) / 100 = $1,000
In this example, the simple interest on the loan amounts to $1,000.
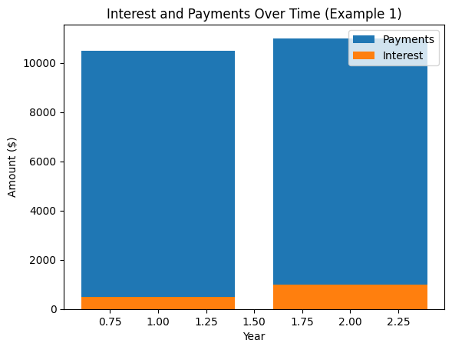
Example #2: Calculating Simple Interest on a Variable-Rate Loan
Let’s consider a variable-rate loan where the interest rate changes annually. Assume a principal of $15,000, with an initial interest rate of 4% in the first year, 5% in the second year, and 6% in the third year.
Step 1: Principal = $15,000
Step 2: Interest Rate = 4% = 0.04 (decimal form)
Step 3: Time = 1 year
Year 1:
Simple Interest for Year 1 = (15,000 × 0.04 × 1) / 100 = $600
Year 2:
Interest Rate = 5% = 0.05 (decimal form)
Time = 1 year
Simple Interest for Year 2 = (15,000 × 0.05 × 1) / 100 = $750
Year 3:
Interest Rate = 6% = 0.06 (decimal form)
Time = 1 year
Simple Interest for Year 3 = (15,000 × 0.06 × 1) / 100 = $900
Total Simple Interest = $600 + $750 + $900 = $2,250
In this example, the total simple interest over the three years would amount to $2,250.
Compound Interest Calculation
Formula for Compound Interest
The compound interest formula is as follows:
A = P(1 + r/n)^(nt)
Where:
A = Total amount (including principal and interest)
P = Principal amount
r = Annual interest rate (expressed as a decimal)
n = Number of times interest is compounded per year
t = time in years
Step-by-Step Calculation Process
- Determine the principal amount, annual interest rate, compounding frequency, and period.
- Convert the annual interest rate into a decimal form.
- Divide the annual interest rate by the compounding frequency to obtain the periodic interest rate.
- Multiply the number of compounding periods per year by the loan term to calculate the total number of compounding periods.
- Apply the compound interest formula to calculate the total amount.
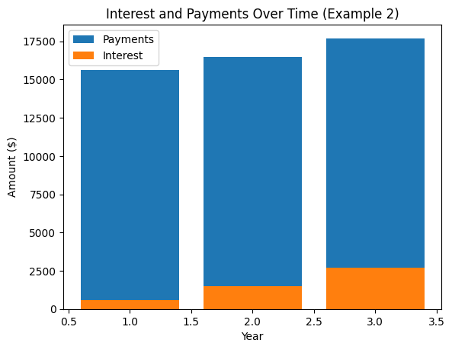
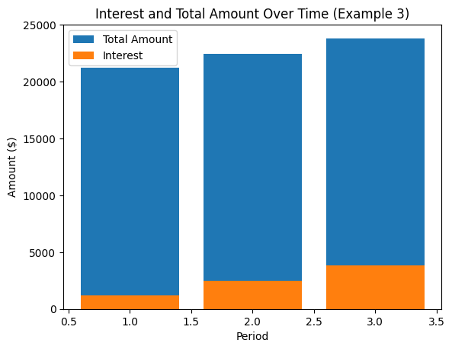
Example #3: Calculating Compound Interest on a Fixed-Rate Loan
Let’s consider a scenario where you borrow $20,000 at an annual interest rate of 6% compounded annually for 3 years.
Step 1: Principal = $20,000
Step 2: Annual Interest Rate = 6% = 0.06 (decimal form)
Step 3: Compounding Frequency = 1 (annually)
Step 4: Time = 3 years
Total Amount (including principal and interest) = 20,000 × (1 + 0.06/1)^(1 × 3) = $22,458.24
In this example, the total amount to be repaid at the end of the loan term, including principal and compound interest, would be approximately $22,458.24.
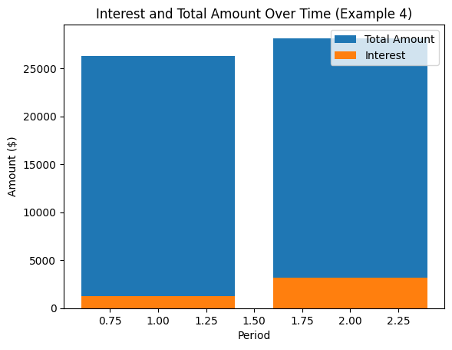
Example #4: Calculating Compound Interest on a Variable-Rate Loan
Let’s consider a variable-rate loan where the interest rate changes semi-annually. Assume a principal of $25,000, with an initial interest rate of 5% in the first six months and 6% in the second six months. The interest is compounded semi-annually for 2 years.
Step 1: Principal = $25,000
Step 2: Annual Interest Rate for the first six months = 5% = 0.05 (decimal form)
Step 3: Compounding Frequency = 2 (semi-annually)
Step 4: Time = 2 years
Number of compounding periods = 2 × 2 = 4
Total Amount (including principal and interest) = 25,000 × (1 + 0.05/2)^(2 × 4) = $28,232.77
In this example, the total amount to be repaid at the end of the two-year term, including principal and compound interest, would be approximately $28,232.77.
Amortization and Loan Payment Schedules
Amortization Definition and Purpose
Amortization is gradually paying down a loan obligation’s principal and interest portions through consistent payments. Assuring that the loan is fully repaid within the specified term is the aim of amortization.
Creating an amortization schedule
Each payment made over the loan term is detailed in an amortization schedule. It specifies how much of each payment goes toward principal and interest and how much of the loan is still owed after each payment.
Impact of Amortization on Interest Calculation
A more significant share of the payment is applied to interest in the early months of the loan period, while a smaller amount is put toward the principal. The percentage of the loan that is assigned to the principal gradually rises as the loan proceeds, lowering the outstanding balance and, consequently, the interest rate.
Loan Payment Schedule Example
Consider a $30,000 loan with a 5-year term and a 7% annual interest rate. Monthly payments are required for the loan’s repayment.
An amortization plan for this loan would give a breakdown of monthly payments, showing how much goes toward principal and interest and how much is left over. It would demonstrate how the outstanding balance over time has gradually decreased.
Factors Affecting Loan Interest Calculation
- Principal Amount: The principal amount significantly impacts how much interest is charged. The cost of interest rises with principle size.
- Interest Rate: The amount of interest charged is directly impacted by the interest rate. Throughout the loan, higher interest rates translate into higher interest costs.
- Loan Term: The overall interest paid depends on the loan period. Shorter loan durations typically lower interest costs, while longer loan terms usually result in higher interest rates.
- Frequency of Compounding: The amount of interest charged depends on how often interest is compounded. Higher interest expenses may be the result of more frequent compounding.
- Additional fees: Loans may also include other costs besides interest, such as origination fees, prepayment fines, or late payment penalties. These fees should be considered when figuring out the overall cost of borrowing.
Key Pointers
- Interest on a loan is calculated based on the principal, interest rate, and time period.
- Simple interest formula: Simple Interest = (Principal * Interest Rate * Time) / 100.
- Compound interest formula: A = P(1 + r/n)^(nt).
- Examples demonstrate the calculation of interest on a loan using both formulas.
- Loan calculators simplify the calculation process and save time.

